Search in Rotated Sorted Array
Suppose a sorted array is rotated at some pivot unknown to you beforehand.
(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).
You are given a target value to search. If found in the array return its index, otherwise return -1.
You may assume no duplicate exists in the array.
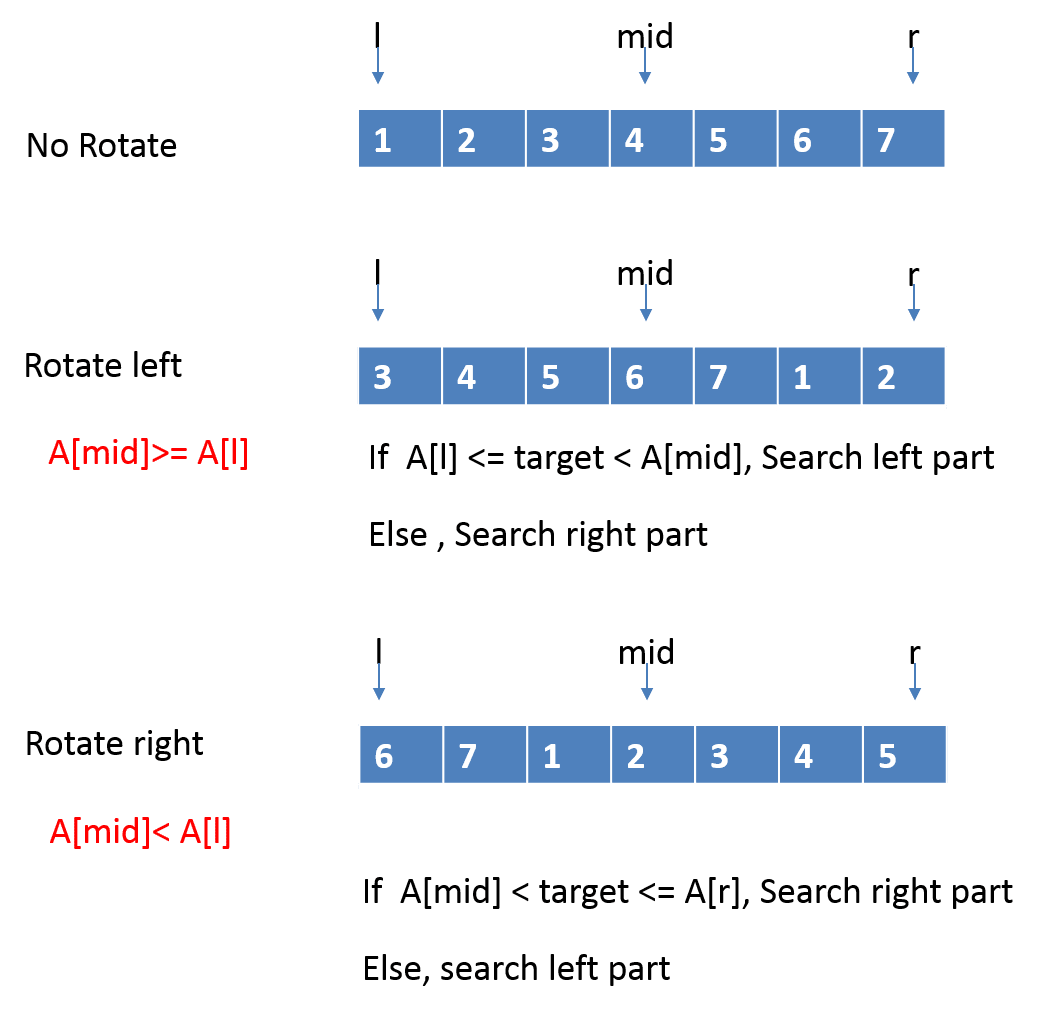
Analysis:
public class Solution {
public int search(int[] A, int target) {
int l = 0;
int r = A.length - 1;
while (l <= r) {
int m = (l + r) / 2;
if (A[m] == target) {
return m;
}
if (A[m] >= A[l]) {
if (A[l] <= target && target < A[m]) {
r = m - 1;
} else {
l = m + 1;
}
} else {
if (A[m] < target && target <= A[r]) {
l = m + 1;
} else {
r = m - 1;
}
}
}
return -1;
}
}
Note:
sdfsdfweerwr
Search in Rotated Sorted Array II
Follow up for “Search in Rotated Sorted Array”:
What if duplicates are allowed?
Would this affect the run-time complexity? How and why?
Write a function to determine if a given target is in the array.