Undirected Graph
1. BFS
2. Union Find
Directed Graph
1. Tarjan
https://www.byvoid.com/blog/scc-tarjan
Undirected Graph
1. BFS
2. Union Find
Directed Graph
1. Tarjan
https://www.byvoid.com/blog/scc-tarjan
http://stackoverflow.com/questions/870218/b-trees-b-trees-difference
1. with target outside the array
public int partitionArray(int[] nums, int k) {
if (nums == null || nums.length == 0) {
return 0;
}
int left = 0;
int right = nums.length - 1;
while (left <= right) {
while (left <= right && nums[left] < k) {
left++;
}
while (left <= right && nums[right] >= k) {
right--;
}
if (left < right) {
swap(nums, left, right);
left++;
right--;
}
}
return left;
}
public void swap(int[] nums, int a, int b) {
int tmp = nums[a];
nums[a] = nums[b];
nums[b] = tmp;
}
2. with target with in the array(Quick select)
Dynamo: Amazon’s Highly Available Key-value Store
|
Problem |
Technique |
Advantage |
|
Partitioning |
Consistent Hashing |
Incremental Scalability |
|
High Availability for writes |
Vector clocks with reconciliation during reads |
Version size is decoupled from update rates. |
|
Handling temporary failures |
Sloppy Quorum and hinted handoff |
Provides high availability and durability guarantee when some of the replicas are not available. |
|
Recovering from permanent failures |
Anti-entropy using Merkle trees |
Synchronizes divergent replicas in the background. |
|
Membership and failure detection |
Gossip-based membership protocol and failure detection. |
Preserves symmetry and avoids having a centralized registry for storing membership and node liveness information. |
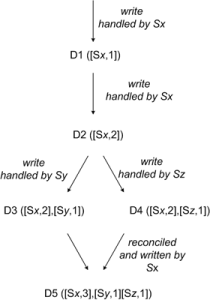
Reference: http://blog.ddup.us/2011/11/07/amazon-dynamo/
Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.
Example
Given the string = "abcdzdcab", return "cdzdc".
Challenge
O(n2) time is acceptable. Can you do it in O(n) time.
Solution1. DP O(n^2)
定义函数
P[i,j] = 字符串区间[i,j]是否为palindrome.
首先找个例子,比如S=”abccb”,
S= a b c c b
Index = 0 1 2 3 4
P[0,0] =1 //each char is a palindrome
P[0,1] =S[0] == S[1] , P[1,1] =1
P[0,2] = S[0] == S[2] && P[1,1], P[1,2] = S[1] == S[2] , P[2,2] = 1
P[0,3] = S[0] == S[3] && P[1,2], P[1,3] = S[1] == S[3] && P[2,2] , P[2,3] =S[2] ==S[3], P[3,3]=1
………………….
由此就可以推导出规律
P[i,j] = 1 if i ==j
= S[i] ==S[j] if j = i+1
= S[i] == S[j] && P[i+1][j-1] if j>i+1
实现如下:
public String longestPalindrome(String s) {
if (s == null) {
return "";
}
String res = "";
int n = s.length();
boolean[][] dp = new boolean[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) {
if (i - j <= 2) {
dp[j][i] = s.charAt(i) == s.charAt(j);
} else {
dp[j][i] = s.charAt(i) == s.charAt(j) && dp[j + 1][i - 1];
}
if (dp[j][i]) {
if (i - j + 1 > res.length()) {
res = s.substring(j, i + 1);
}
}
}
}
return res;
}
Solution2: Check both aba and abba 2 cases. O(n^2)
public String longestPalindrome(String s) {
if (s == null || s.length() == 0) {
return "";
}
String result = "";
//1. if it is like 'aba'
for (int i = 0; i < s.length(); i++) {
int count = 0;
while (i - count >= 0 && i + count < s.length() && s.charAt(i - count) == s.charAt(i + count)) {
count++;
}
String palindrome = s.substring(i - count + 1, i + count);
if (palindrome.length() > result.length()) {
result = palindrome;
}
}
//2. if it is like 'abba', the pivot would be the interval between i and i+1
for (int i = 0; i < s.length() - 1; i++) {
int count = 1;
while (i - count + 1 >= 0 && i + count < s.length() && s.charAt(i - count + 1) == s.charAt(i + count)) {
count++;
}
if (count > 1) {
String palindrome = s.substring(i - count + 2, i + count);
if (palindrome.length() > result.length()) {
result = palindrome;
}
}
}
return result;
}
Given k strings, find the longest common prefix (LCP).
Example
For strings "ABCD", "ABEF" and "ACEF", the LCP is "A"
For strings "ABCDEFG", "ABCEFG" and "ABCEFA", the LCP is "ABC"
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
String lcp = strs[0];
for (int i = 1; i < strs.length; i++) {
lcp = getLCP(lcp, strs[i]);
}
return lcp;
}
public String getLCP(String s1, String s2) {
StringBuilder sb = new StringBuilder();
int n = Math.min(s1.length(), s2. length());
for (int i = 0; i < n; i++) {
if (s1.charAt(i) == s2.charAt(i)) {
sb.append(s1.charAt(i));
} else {
break;
}
}
return sb.toString();
}