A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

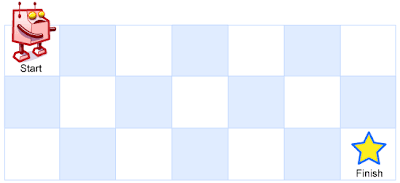
Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

Version 1. Initialize first row and first column separately

    public int uniquePaths(int m, int n) {
    	if (m <= 0 || n <= 0) {
    		return 0;
    	}
    	int[][] f = new int[m][n];
    	//initialize the first column
    	for (int i = 0; i < m; i++) {
    		f[i][0] = 1;
    	}
    	//initialize the first row
    	for (int j = 0; j < n; j++) {
    		f[0][j] = 1;
    	}
    	for (int i = 1; i < m; i++) {
    		for (int j = 1; j < n; j++) {
    			f[i][j] = f[i - 1][j] + f[i][j - 1];
    		}
    	}
    	return f[m - 1][n - 1];
    }

Version 2. Put initialization in the 2 for loop.

public class Solution {
   public int uniquePaths(int m, int n) {
        if (m <= 0 || n <= 0) {
            return 0;
        }
        int[][] pathMap = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 || j == 0) {
                    pathMap[i][j] = 1;
                } else if (pathMap[i][j] == 0) {
                    pathMap[i][j] = pathMap[i - 1][j] + pathMap[i][j - 1];
                }
            }
        }
        return pathMap[m - 1][n - 1];
    }
}

Share