Ref:
Java Thread: notify() and wait() examples
How to Work With wait(), notify() and notifyAll() in Java?
1. Keywords & Methods:
- Synchronized
synchronized keyword is used for exclusive accessing.- To make a method synchronized, simply add the synchronized keyword to its declaration. Then no two invocations of synchronized methods on the same object can interleave with each other.
- wait()
- notify()
- notifyAll()
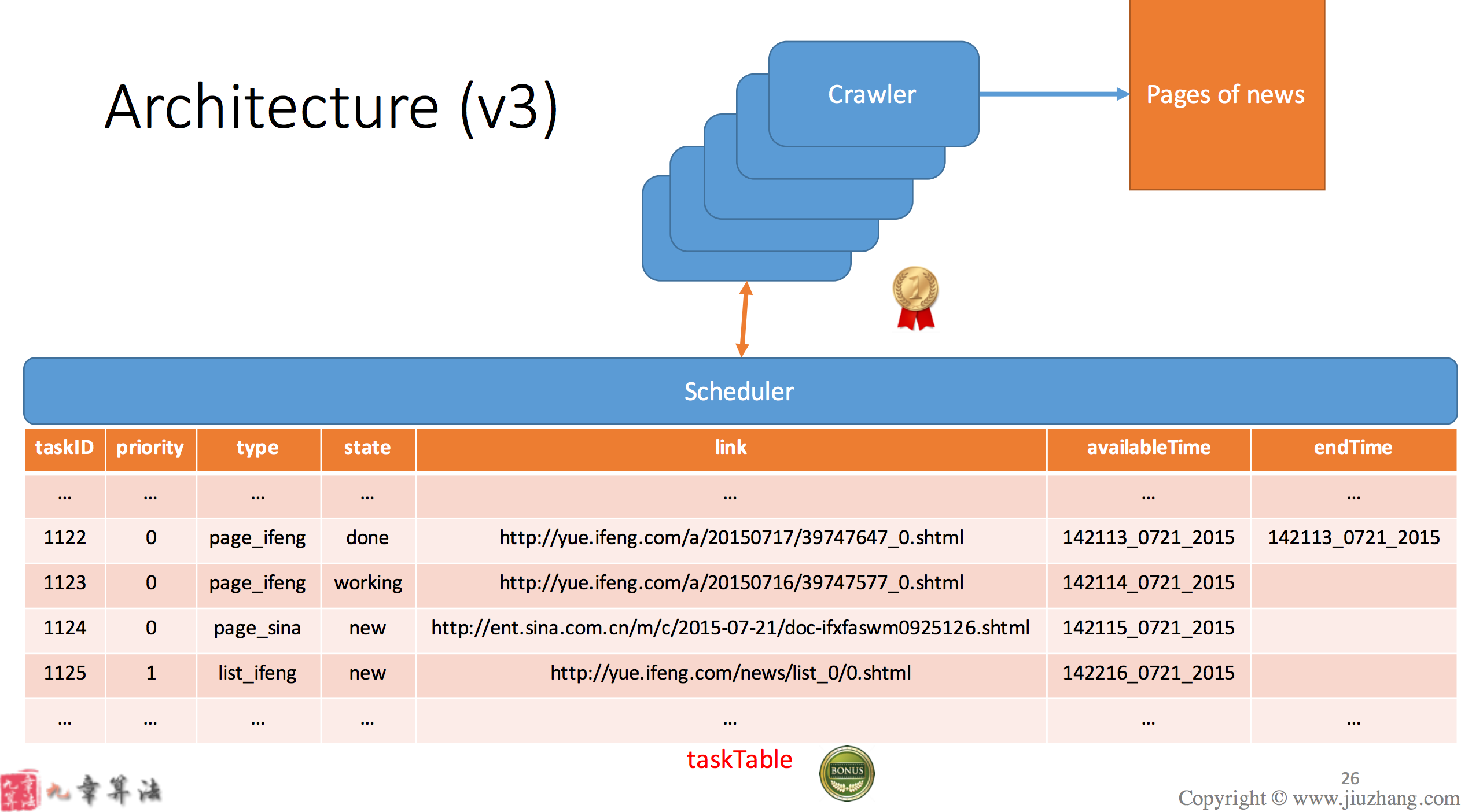
2. Example
Producer and Consumer:
1) Producer thread produce a new resource in every 1 second and put it in ‘taskQueue’.
2) Consumer thread takes 1 seconds to process consumed resource from ‘taskQueue’.
3) Max capacity of taskQueue is 5 i.e. maximum 5 resources can exist inside ‘taskQueue’ at any given time.
4) Both threads run infinitely.
Producer:
public class Producer implements Runnable {
private List<Integer> taskQueue;
private int MAX_CAPACITY;
//instead of having an int counter,
//we use a wrapper object, so that it can be passed by reference
private Counter counter;
public Producer(List<Integer> taskQueue, int max_capacity, Counter counter) {
this.taskQueue = taskQueue;
this.MAX_CAPACITY = max_capacity;
this.counter = counter;
}
@Override
public void run() {
//infinite loop so that producer keeps producing elements at regular interval.
while (true) {
synchronized (taskQueue) {
try {
//here it has to be while instead of if since if after it is waken up,
//someone else takes the lock and change the taskQueue size
//if check will still go through and start producing
while (taskQueue.size() == MAX_CAPACITY) {
System.out.println(Thread.currentThread().getName() +
": Queue(size=" + taskQueue.size() + ")is full, now start waiting...");
taskQueue.wait();
}
//simulating time delays in consuming elements.
Thread.sleep(100);
taskQueue.add(counter.val);
System.out.println(Thread.currentThread().getName() + ": Produced:" + counter.val);
counter.increase();
//Calling notifyAll() because the last-time wait() method was called by consumer thread
//(that’s why producer is out of waiting state), consumer gets the notification.
taskQueue.notifyAll();
} catch (InterruptedException e) {
e.printStackTrace();
}
}
//do something else
}
}
}
1) Here “produce(counter++)” code has been written inside infinite loop so that producer keeps producing elements at regular interval.
2) We have written the produce() method code following the general guideline to write wait() method as mentioned in first section.
3) Once the wait() is over, producer add an element in taskQueue and called notifyAll() method. Because the last-time wait() method was called by consumer thread (that’s why producer is out of waiting state), consumer gets the notification.
4) Consumer thread after getting notification, if ready to consume the element as per written logic.
5) Note that both threads use sleep() methods as well for simulating time delays in creating and consuming elements.
Consumer:
public class Consumer implements Runnable {
private List<Integer> taskQueue;
public Consumer(List<Integer> taskQueue) {
this.taskQueue = taskQueue;
}
@Override
public void run() {
//infinite loop so that consumer keeps consuming elements whenever it finds something in taskQueue..
while (true) {
synchronized (taskQueue) {
try {
while (taskQueue.size() == 0) {
System.out.println(Thread.currentThread().getName() +
": Queue(size=" + taskQueue.size() + ")is empty, now start waiting...");
taskQueue.wait();
}
//simulating time delays in consuming elements.
Thread.sleep(100);
System.out.println(Thread.currentThread().getName() + ": consuming " + taskQueue.remove(0));
//Once the wait() is over, consumer removes an element in taskQueue and called notifyAll() method.
//Because the last-time wait() method was called by producer thread
//(that’s why producer is in waiting state), producer gets the notification.
taskQueue.notifyAll();
} catch (InterruptedException e) {
e.printStackTrace();
}
}
//do something else
}
}
}
1) Here “consume()” code has been written inside infinite loop so that consumer keeps consuming elements whenever it finds something in taskQueue..
2) Once the wait() is over, consumer removes an element in taskQueue and called notifyAll() method. Because the last-time wait() method was called by producer thread (that’s why producer is in waiting state), producer gets the notification.
3) Producer thread after getting notification, if ready to produce the element as per written logic.
Counter:
Noted that we need a counter as an id for each task. Since we might need more than one producer, instead of passing int or Integer(both of them are immutable), we need to have a wrapper object so that we can pass by reference to be shared between multiple producers.
public class Counter {
int val;
public Counter(){
val = 0;
}
public void increase(){
val++;
}
public void decrease(){
val--;
}
}
Test:
public class ProducerConsumer {
public static void main(String[] args) {
Counter c = new Counter();
List<Integer> taskQueue = new ArrayList<>();
Thread tProducer1 = new Thread(new Producer(taskQueue, 5, c), "Producer1");
Thread tProducer2 = new Thread(new Producer(taskQueue, 5, c), "Producer2");
Thread tConsumer1 = new Thread(new Consumer(taskQueue), "Consumer1");
Thread tConsumer2 = new Thread(new Consumer(taskQueue), "Consumer2");
tProducer1.start();
tProducer2.start();
tConsumer1.start();
tConsumer2.start();
}
}
Output:
Producer1: Produced:0
Producer1: Produced:1
Consumer2: consuming 0
Consumer2: consuming 1
Consumer1: Queue(size=0)is empty, now start waiting…
Producer2: Produced:2
Consumer1: consuming 2
Consumer2: Queue(size=0)is empty, now start waiting…
Producer1: Produced:3
Consumer2: consuming 3
Consumer1: Queue(size=0)is empty, now start waiting…
Consumer2: Queue(size=0)is empty, now start waiting…
Producer2: Produced:4
Consumer2: consuming 4
Consumer2: Queue(size=0)is empty, now start waiting…
Consumer1: Queue(size=0)is empty, now start waiting…
Producer1: Produced:5
Producer1: Produced:6
Producer1: Produced:7
Producer1: Produced:8
Producer1: Produced:9
Producer1: Queue(size=5)is full, now start waiting…
Consumer1: consuming 5
Consumer2: consuming 6
Consumer2: consuming 7
Consumer2: consuming 8
Consumer2: consuming 9
Consumer2: Queue(size=0)is empty, now start waiting…