|
Property
|
HashMap
|
Hashtable
|
LinkedHashMap
|
TreeMap
|
|
|
1
|
Insertion order
|
HashMap does not maintains insertion order in java.
|
Hashtable does not maintains insertion order in java.
|
LinkedHashMap maintains insertion order in java.
|
TreeMap is sorted by natural order of keys in java.
|
|
2
|
Performance
|
HashMap is not synchronized, hence its operations are faster as compared to Hashtable.
|
Hashtable is synchronized, hence its operations are slower as compared HashMap.
If we are working not working in multithreading environment jdk recommends us to use HashMap.
|
LinkedHashMap must be used only when we want to maintain insertion order. Time and space overhead is there because for maintaining order it internally uses Doubly Linked list.
|
TreeMap must be used only when we want sorting based on natural order. Otherwise sorting operations cost performance. (Comparator is called for sorting purpose)
|
|
3
|
Null keys and values
|
HashMap allows to store one null key and many null values i.e. many keys can have null value in java.
|
Hashtable does not allow to store null key or null value.
Any attempt to store null key or value throws runtimeException (NullPointerException) in java.
|
LinkedHashMap allows to store one null key and many null values i.e. any key can have null value in java.
|
TreeMap does not allow to store null key but allow many null values.
Any attempt to store null key throws runtimeException (NullPointerException) in java.
|
|
4
|
Implements which interface
|
HashMap implements java.util.Map
|
Hashtable implements java.util.Map
|
LinkedHashMap implements java.util.Map
|
TreeMap implements
java.util.Map
java.util.SortedMap
java.util.NavigableMap
|
|
5
|
Implementation uses?
|
HashMap use buckets
|
Hashtable use buckets
|
LinkedHashMap uses doubly linked lists
|
TreeMap uses Red black tree
|
|
6
|
Complexity of put, get and remove methods
|
O(1)
|
O(1)
|
O(1)
overhead of updating Doubly Linked list for maintaining order it internally uses.
|
O(log(n))
|
|
7
|
Extends java.util.Dictionary (Abstract class, which is obsolete)
|
HashMap doesn’t extends Dictionary.
|
Hashtable extends Dictionary (which maps non-null keys to values. In a given Dictionary we can look up value corresponding to key)
|
LinkedHashMap doesn’t extends Dictionary.
|
TreeMap doesn’t extends Dictionary.
|
|
8
|
Introduced in which java version?
|
HashMap was introduced in second version of java i.e. JDK 2.0
|
Hashtable was introduced in first version of java i.e. JDK 1.0
But it was refactored in java 2 i.e. JDK 1.2 to implement the Map interface, hence making it a member of member of the Java Collections Framework.
|
LinkedHashMap was introduced in fourth version of java i.e. JDK 4.0
|
TreeMap was introduced in second version of java i.e. JDK 2.0
|
Author Archives: Ying
sdfsf
sdfsfsf
Leetcode: 349. Intersection of Two Arrays
Given two arrays, write a function to compute their intersection.
Example:
Given nums1 = [1, 2, 2, 1], nums2 = [2, 2], return [2].
Note:
- Each element in the result must be unique.
- The result can be in any order.
public int fourSumCount(int[] A, int[] B, int[] C, int[] D) {
int count = 0;
HashMap<Integer, Integer> twoSum1 = new HashMap<>();
HashMap<Integer, Integer> twoSum2 = new HashMap<>();
constructTwoPairMap(twoSum1, A, B);
constructTwoPairMap(twoSum2, C, D);
for (Integer pairSum : twoSum1.keySet()) {
count += twoSum1.get(pairSum) * twoSum2.getOrDefault(pairSum * (-1), 0);
}
return count;
}
public void constructTwoPairMap(HashMap<Integer, Integer> map, int[] A, int[] B) {
for (int i = 0; i < A.length; i++) {
for (int j = 0; j < B.length; j++) {
int sum = A[i] + B[j];
map.put(sum, map.getOrDefault(sum, 0) + 1);
}
}
}
Bit Manipulation
1. Extract the last set bit
x & (-x)
eg. x: 00110010
-x: 11001101 + 1 = 11001110
x & (-x) = 00000010
2. Remove the last set bit
x – x & (-x)
TCP VS UDP
UDP (User Datagram Protocol) – Light wight but not that reliable
Pros:
1. Packets size is smaller than TCP (udp header: 8 bytes vs tcp header 20bytes)
2. No connections to create and maintain
3. More control on when the data is sent
Cons:
1. No error recovery. lost packets are just discarded.
2. Packets can arrive out of order
3. No traffic control.
4. Optional checksum in IPv4, only mandatory in IPv6
TCP (Transmission Control Protocol) – Reliable but bigger communication overhead
3 way handshake
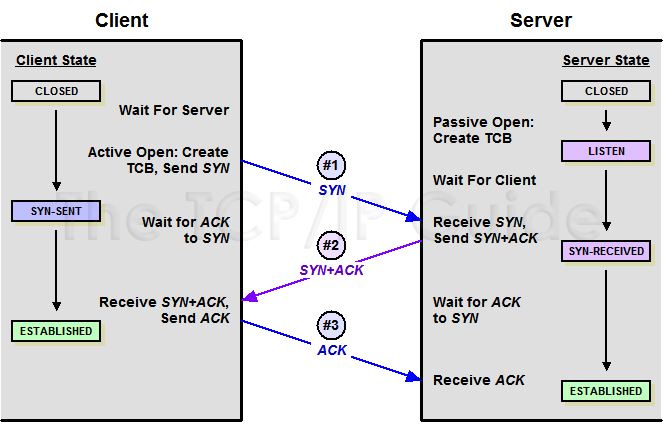
Pros:
1. Delivery acknowledgement. Receiver would send a respond confirming the packets has been received.
2. Retransmission. When the sender doesn’t get the confirmation from the receiver after a certain amount of time, it will resent the packets.
3. Traffic control. TCP delays transmission if the network is congested.
4. Checksum is now mandatory for both IPv6 and IPv4
Cons:
1. Bigger header
2. Data doesn’t always get sent out immediately (think of video conferencing)
3. Bigger traffic overhead (because of the retransmission and delivery acknowledgement)
Dungeon Game
The demons had captured the princess (P) and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of M x N rooms laid out in a 2D grid. Our valiant knight (K) was initially positioned in the top-left room and must fight his way through the dungeon to rescue the princess.
The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately.
Some of the rooms are guarded by demons, so the knight loses health (negative integers) upon entering these rooms; other rooms are either empty (0’s) or contain magic orbs that increase the knight’s health (positive integers).
In order to reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step.
Write a function to determine the knight’s minimum initial health so that he is able to rescue the princess.
For example, given the dungeon below, the initial health of the knight must be at least 7 if he follows the optimal path RIGHT-> RIGHT -> DOWN -> DOWN.
| -2 (K) | -3 | 3 |
| -5 | -10 | 1 |
| 10 | 30 | -5 (P) |
Notes:
- The knight’s health has no upper bound.
- Any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.
public int calculateMinimumHP(int[][] dungeon) {
if (dungeon == null || dungeon.length == 0 || dungeon[0].length == 0) {
return 0;
}
int row = dungeon.length;
int col = dungeon[0].length;
//dp[i][j]: the minimum hp knight need to have at dungeon[i][j]
int[][] dp = new int[row][col];
//init bottom-right cell
dp[row - 1][col - 1] = Math.max(1 - dungeon[row - 1][col - 1], 1);
//init rightmost rooms
for (int i = row - 2; i >= 0; i--) {
dp[i][col - 1] = Math.max(dp[i + 1][col - 1] - dungeon[i][col - 1], 1);
}
//init bottom rooms
for (int j = col - 2; j >= 0; j--) {
dp[row - 1][j] = Math.max(dp[row - 1][j + 1] - dungeon[row - 1][j], 1);
}
//dp
for (int i = row - 2; i >= 0; i--) {
for (int j = col - 2; j >= 0; j--) {
dp[i][j] = Math.max(Math.min(dp[i][j + 1] - dungeon[i][j], dp[i + 1][j] - dungeon[i][j]), 1);
}
}
return dp[0][0];
}
Phone Screen @Uber Oct. 26th, 2015
Given a pattern and an input string, check if the input string matches the pattern.
Eg.
pattern: abab
input: howwhathowwhat
mapping: a => how, b => what
so match(abab, howwhathowwhat) -> true
match(abab, whathowhowwhat) -> false
match(“”, “”) -> true
match(“a”, “a”) -> true
match(“ab”, “abab”) -> true
match(“aaaa”, “howwhatwhathow”) -> false
match(“aaaa”, “whatwhatwhatwhat”) -> true
Each char in pattern string can match 1-n chars in input string. Same char can only match same string. Different chars can match same strings.
class Solution {
public boolean match(String pattern, String input) {
if (pattern == null || input == null || input.length() < pattern.length()) {
return false;
}
Map<Character, String> map = new HashMap<>();
return matchHelper(pattern, 0, input, 0, map);
}
public boolean matchHelper(String pattern, int index, String input, int inputIndex, Map<Character, String> map) {
if (index == pattern.length()) {
if (inputIndex == input.length()) {
return true;
}
return false;
}
char c = pattern.charAt(index);
if (map.containsKey(c)) {
String val = map.get(c);
if (inputIndex + val.length() <= input.length() && val.equals(input.substring(inputIndex, inputIndex + val.length()))) {
return matchHelper(pattern, index + 1, input, inputIndex + val.length(), map);
}
} else {
for (int i = inputIndex; i < input.length(); i++) {
String val = input.substring(inputIndex, i + 1);
map.put(c, val);
if (matchHelper(pattern, index + 1, input, i + 1, map)) {
return true;
}
map.remove(c);
}
}
return false;
}
public static void main(String[] args) {
Solution s = new Solution();
System.out.println(s.match("", "")); //true
System.out.println(s.match("a", "a")); //true
System.out.println(s.match("ab", "abab")); //true
System.out.println(s.match("abab", "howwhathowwhat")); //true
System.out.println(s.match("abab", "howwhatwhathow")); //false
System.out.println(s.match("aaaa", "howwhatwhathow")); //false
System.out.println(s.match("aaaa", "whatwhatwhatwhat")); //true
}
}
Sqrt(x)
Implement int sqrt(int x).
Compute and return the square root of x.
Example
sqrt(3) = 1
sqrt(4) = 2
sqrt(5) = 2
sqrt(10) = 3
O(log(x))
Solution: Binary search O(log(x)). Remember to use Long during computation
public int sqrt(int x) {
// find the last number which square of it <= x
long start = 1, end = x;
while (start + 1 < end) {
long mid = start + (end - start) / 2;
if (mid * mid <= x) {
start = mid;
} else {
end = mid;
}
}
if (end * end <= x) {
return (int) end;
}
return (int) start;
}
Mid Stack
http://www.geeksforgeeks.org/design-a-stack-with-find-middle-operation/
Shortest Word Distance I, II & III
Word Distance I – Only called once
Given a list of words and two words word1 and word2, return the shortest distance between these two words in the list.
For example,
Assume that words = ["practice", "makes", "perfect", "coding", "makes"].
Given word1 = “coding”, word2 = “practice”, return 3.
Given word1 = "makes", word2 = "coding", return 1.
Note:
You may assume that word1 does not equal to word2, and word1 and word2 are both in the list.
Solution: One pass. O(n), Every time find an occurrence of word1 or word2, compare the distance of p1 and p2.
public int shortestDistance(String[] words, String word1, String word2) {
int p1 = -1, p2 = -1, min = Integer.MAX_VALUE;
for (int i = 0; i < words.length; i++) {
if (words[i].equals(word1))
p1 = i;
if (words[i].equals(word2))
p2 = i;
if (p1 != -1 && p2 != -1)
min = Math.min(min, Math.abs(p1 - p2));
}
return min;
}
Shortest Word Distance II – API, will be called multiple times
This is a follow up of Shortest Word Distance. The only difference is now you are given the list of words and your method will be called repeatedly many times with different parameters. How would you optimize it?
Design a class which receives a list of words in the constructor, and implements a method that takes two words word1 and word2 and return the shortest distance between these two words in the list.
For example,
Assume that words = ["practice", "makes", "perfect", "coding", "makes"].
Given word1 = “coding”, word2 = “practice”, return 3.
Given word1 = "makes", word2 = "coding", return 1.
Note:
You may assume that word1 does not equal to word2, and word1 and word2 are both in the list.
Solution: First preprocess the word to dict, which is a <word, list of index>map.
Then every time just get the word only check two list of indexes.
public class WordDistance {
Map<String, List<Integer>> dict;
public WordDistance(String[] words) {
dict = new HashMap<>();
for(int i=0;i<words.length;i++){
if(dict.containsKey(words[i])){
dict.get(words[i]).add(i);
}else{
List<Integer> indexes = new ArrayList<>();
indexes.add(i);
dict.put(words[i], indexes);
}
}
}
public int shortest(String word1, String word2) {
if(dict==null||!dict.containsKey(word1)||!dict.containsKey(word2)){
return 0;
}
int res = Integer.MAX_VALUE;
List<Integer> indexes1 = dict.get(word1);
List<Integer> indexes2 = dict.get(word2);
int index1 = 0;
int index2 = 0;
while(index1<indexes1.size()&&index2<indexes2.size()){
res = Math.min(res, Math.abs(indexes1.get(index1)-indexes2.get(index2)));
if(indexes1.get(index1)<indexes2.get(index2)){
index1++;
}else{
index2++;
}
}
return res;
}
}
Shortest Word Distance III – word1 could be the same as word2
This is a follow up of Shortest Word Distance. The only difference is now word1 could be the same as word2.
Given a list of words and two words word1 and word2, return the shortest distance between these two words in the list.
word1 and word2 may be the same and they represent two individual words in the list.
For example,
Assume that words = ["practice", "makes", "perfect", "coding", "makes"].
Given word1 = “makes”, word2 = “coding”, return 1.
Given word1 = "makes", word2 = "makes", return 3.
Note:
You may assume word1 and word2 are both in the list.
Solution: if word1==word2==words[], then p1=p2=i, and every time we update p1, we check the distance between p1 and p2.
public int shortestWordDistance(String[] words, String word1, String word2) {
int p1 = -1, p2 = -1, min = Integer.MAX_VALUE;
for (int i = 0; i < words.length; i++) {
if (words[i].equals(word1)) {
p1 = i;
if (word1.equals(word2) && p1 != -1 && p2 != -1) {
min = Math.min(min, Math.abs(p1 - p2));
}
}
if (words[i].equals(word2)) {
p2 = i;
}
if (!word1.equals(word2) && p1 != -1 && p2 != -1) {
min = Math.min(min, Math.abs(p1 - p2));
}
}
return min;
}